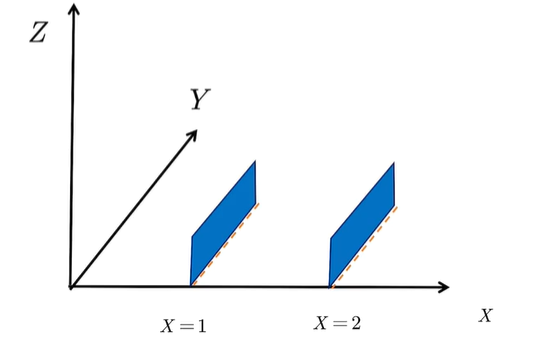
独立、均值独立与线性不相关

独立

两个随机变量 x 和 y，满足 f(x) \times f(y) = f(x,y)，则称随机变量 x 和 y 独立。从图像上来理解，就是对任意的 x，f_{Y|X}(y|x) 都是相同的，所以 x 不会带来任何新的信息。

独立

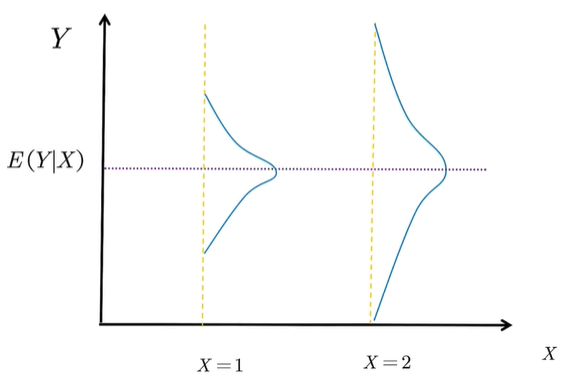
均值独立

对随机变量 x 和 y，若 E(y|x) = E(y)，则称随机变量 y 均值独立于随机变量 x。从图像上来理解，就是任意给定 x，f_{Y|X} 的条件期望是一样的，分布可以不一样。

均值独立

线性不相关

若随机变量 x 和 y 协方差为 0，则称随机变量 x 和 y 线性无关。

三者间的关系

从条件强度来说，独立 > 均值独立 > 线性不相关。

引理 1：迭代期望法则

E[Y] = E[E[Y|X]]

证明：

\begin{split} E[E[Y|X]] &= \int{\int{y f_{Y|X}(y|x)dy}f_X(x)dx} \\ &= \int{\int{y \frac{f_{X,Y}(x,y)}{f_{X}(x)} dy}f_X(x)dx} \\ &= \int{\int{y f_{X,Y}(x,y)dy}dx} \\ &= \int{\int{f_{X,Y}(x,y)dx}ydy} \\ &= \int{y f_{Y}(y)dy} \\ &= E[Y] \end{split}

引理 2：协方差与条件期望法则

Cov[X,Y] = Cov[X, E[Y|X]]

证明：

\begin{split} Cov[X, E[Y|X]] &= E[XE[Y|X]] - E[X]E[E[Y|X]] \\ &= \int{xf_{X}(x) \int{yf_{Y|X}(y|x)dy}dx} - E[X]E[Y] \\ &= \int{xf_{X}(x) \int{y \frac{f_{X,Y}(x,y)}{f_{X}(x)}dy}dx} - E[X]E[Y] \\ &= \int{\int{xy f_{X,Y}(x,y)dy}dx} - E[X]E[Y] \\ &= E[XY] - E[X]E[Y] \\ &= Cov[X,Y] \end{split}

由均值独立推出线性不相关

\begin{split} Cov(X,Y) &= E[XY] - E[X]E[Y] \\ &= E[E[XY|X]] - E[X]E[Y] \\ &= E[XE[Y|X]] - E[X]E[Y] \\ &= E[XE[Y]] - E[X]E[Y] \\ &= E[X]E[Y] - E[X]E[Y] \\ &= 0 \end{split}